1 Boolesche Algebra und digitale Logik

1.5 Die Grundfunktionen der Digitaltechnik: ODER, UND, NOT

Unter den Booleschen Funktionen mit n = 1 und n = 2 nehmen die Funktionen UND, ODER sowie NOT eine herausragende Stellung ein, weshalb ihre Eigenschaften hier detaillierter diskutiert werden sollen:

1.5.1 Die Boolesche Funktion "ODER"

Der ODER-Funktion (engl. "OR") entspricht in der Mengenlehre die "Vereinigungsmenge" bzw. die Funktion "Disjunktion".

Die Vereinigungsmenge

Abb. 1.14: Venn-Diagramm der ODER-Funktion.

Umfaßt der Venn-Kreis, wie vorher definiert, jeweils den Argumentwert "1", so liefert die Logik-Operation a + b also genau dann eine "1", wenn mindestens ein Argument den Wert "1" besitzt.

Diese "Flächenvereinigung" entspricht also der Funktion

Wie beschrieben, wird in der Digitaltechnik eine Erweiterung auf n > 2 vorgenommen, ohne die Grunddefinition der Booleschen Funktion zu modifizieren.

Damit ergibt sich für die n-fache ODER-Funktion:

• f(x1,x2,...,xn) = x1 x2 ... xn = x1+ x2 + ... + xn,
• f(x1,x2,...,xn) = 1, falls für mindestens ein Argument xi = 1 gilt,

oder (mit gleicher Aussagekraft)

• f(x1,x2,...,xn) = 0, falls für alle Argumente xi = 0 gilt.

Dieser Sachverhalt kann auch in Form einer Wahrheitstafel für n Argumente gefaßt werden:

Auch das Schaltzeichen der n-fachen ODER-Funktion wird in entsprechender Weise von dem 2-fach ODER übernommen:

Abb. 1.15: Schaltzeichen der ODER-Funktion (nach DIN).

Mit Blick auf die technische Realisierung wird die hierdurch implementierte Schaltfunktion als "ODER-Gatter" bezeichnet.

1.5.2 Die Boolesche Funktion "UND"

Der UND-Funktion (engl. "AND") entspricht in der Mengenlehre die "Durchschnittsmenge" bzw. die Funktion "Konjunktion".

Die Durchschnittsmenge

Abb. 1.16: Venn-Diagramm der UND-Funktion.

Die Logik-Operation a·b ergibt demnach genau dann eine "1", wenn beide Argumente den Wert "1" besitzen.

Diese "Flächenüberschneidung" entspricht also der Funktion

Der Übergang zur n-fachen UND-Funktion liefert entsprechend:

• f(x1,x2,...,xn) = x1 x2 ... xn = x1· x2 · ... · xn,
• f(x1,x2,...,xn) = 0, falls für mindestens ein Argument xi = 0 gilt,
  

oder (mit gleicher Aussagekraft)

• f(x1,x2,...,xn) = 1, falls für alle Argumente xi = 1 gilt.
  

Dieser Sachverhalt kann auch hier in Form einer Wahrheitstafel für n Argumente gefaßt werden:

Auch das Schaltzeichen der n-fachen UND-Funktion wird in entsprechender Weise von dem 2-fach UND übernommen:

Abb. 1.17: Schaltzeichen der ODER-Funktion (nach DIN).

Mit Blick auf die technische Realisierung wird die hierdurch implementierte Schaltfunktion als "UND-Gatter" bezeichnet.

1.5.3 Die Boolesche Funktion "NOT"

Die Boolesche Funktion "NOT" (Negation, INVERS-Funktion) wurde bereits in Kapitel 1.3 eingeführt und interpretiert.

Der NOT-Funktion entspricht in der Mengenlehre die "Komplementmenge" bzw. die Funktion "Komplementation".

Diese Funktion stellt eine rein unäre Operation dar, deren Erweiterung auf n Eingangsvariable in dieser Form nicht sinnvoll ist.

In Verbindung mit den n-fachen UND- bzw. ODER-Funktionen nimmt auch diese Funktion allerdings eine Sonderstellung ein (s.u.).

In erweiterter Form kann der Begriff der inversen Funktion eingeführt werden:

Definition:

Zwei Boolesche Funktionen f(x1,x2,...,xn) und g(x1,x2,...,xn) sind zueinander invers, wenn für alle Argument-n-Tupel (x1,x2,...,xn) gilt:

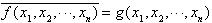(1.4),

Die durch die Inversion vermittelte Abbildung kann wiederum durch Mengen-Diagramme veranschaulicht werden:

Abb. 1.18: Zueinander inverse Boolesche Funktionen.